TD6/1: ISOMETRIC PROJECTIONS AUXILLIARY PROJECTION ASSIGNEMNT

Exercise 10

 (All questions originally set in imperial units.)

Figure 1 shows the elevation of a 20 mm square prism 50 mm long resting with one of its corners on the HP. Draw, full size, the following views and show all the hidden detail. (a) The given elevation. (b) An EE looking in the direction of arrow E . (c) A plan projected beneath view (a). North Western Secondary School Examinations Board 45° 100 125 Dimensions in mm X Y X1 Y1 18 32 φ 38 Figure 3 32 mm 75 mm 50 mm A B C D Figure 2

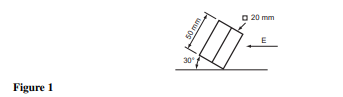
Figure 2 shows the FE and an isometric sketch of a sheet metal foot light reflector for a puppet theatre. Draw, full size, the given FE and from it project the plan and end view of the reflector. Draw, also, the true shape of the surface marked ABCD. The thickness of the metal can be ignored. West Midlands Examinations Board

The plan and elevation of a hexagonal distance piece are shown in Fig. 3 . Draw these views, full size, and project an AE on X 1 Y 1. Hidden details are not to be shown. Associated Lancashire Schools Examining Board www.engbookspdf.com 142 Geometric and Engineering Drawing

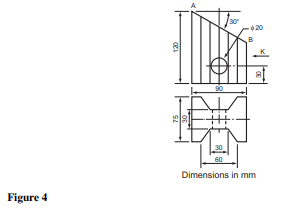
Figure 4 shows details of a cast concrete block. To a scale of 10 mm  100 mm draw the following: (a) The two given views. (b) An EE looking in the direction of the arrow K . (c) The true shape of the sloping surface AB. Metropolitan Regional Examinations Board 2535 50 112 28 37.5 12 25 100 Dimensions in mm 37.5 5 Square sect 30° M 60° X1 Y1 Figure 5

Two views are shown of a bungalow which has been made as a model ( Fig. 5 ). To obtain a better impression of its design a view in the direction of arrow M is required. Draw, full size, the following: (a) The two given views. (b) An AE, projected from the plan, in the direction of arrow M .

The plan and elevation of a special angle bracket are shown in Fig. 14 . (a) Draw, full size, the given views and project an AP on the ground line X 1 – Y 1 . (b) Using the AP in (a) above, project an AE on the ground line X 2 – Y 2 . All hidden detail to be shown. Associated Examining Board 6

Intersection of Regular Solids

When two solids interpenetrate, a line of intersection is formed. It is sometimes necessary to know the exact shape of this line, usually so that an accurate development of either or both of the solids can be drawn. This chapter shows the lines of intersection formed when some of the simpler geometric solids interpenetrate. Two dissimilar square prisms meeting at right angles ( Fig. 12.1 )

1 First angle projection 4 1, 3 2 1 2 3 4 2, 4 3 Figure 12.1 The EE shows where corners 1 and 3 meet the larger prism and these are projected across to the FE The plan shows where corners 2 and 4 meet the larger prism and this is projected up to the FE. www.engbookspdf.com 166 Geometric and Engineering Drawing Two dissimilar square prisms meeting at an angle ( Fig. 12.2 ). TheFE shows where corners 1 and 3 meet the larger prism. The plan shows where corners 2 and 4 meet the larger prism and this is projected down to the FE.

Third angle projection 2 1 4 2 3 4 1 1 2, 4 3 3 Figure 12.2 A hexagonal prism meeting a square prism at right angles ( Fig. 12.3 ). The plan shows where all the corners of the hexagonal prism meet the square prism. These are projected down to the FE to meet the projectors from the same corners on the EE.

3 2, 4 Third angle projection 1, 5 1, 2 1 2 6 3 5 4 3, 6 4, 5 6 Figure 12.3 www.engbookspdf.com Intersection of Regular Solids 167 1 1 6 1, 5 2, 4 3 2 3 4 5 6 First angle projection 2 6 3 5 4 Figure 12.4 Two dissimilar hexagonal prisms meeting at an angle ( Fig. 12.4 ). TheFE shows where corners 3 and 6 meet the larger prism. The plan shows where corners 1, 2, 4 and 5 meet the larger prism and these are projected up to the FE.

Ahexagonal prism meeting an octagonal prism at an angle, their centres not being in the same VP ( Fig. 12.5 ).

Third angle projection 1 2 6 3 a,b 6 5 a b 4 3 2 1 5 4 6 1, 5 2, 4 3 b a Figure 12.5 www.engbookspdf.com 168 Geometric and Engineering Drawing TheFE shows where corners 3 and 6 meet the octagonal prism. The plan shows where corners 1, 2, 4 and 5 meet the octagonal prism and these are projected down to the FE. Thesides of the hexagonal prism between corners 3 – 4 and 5 – 6 meet two sides of the octagonal prism. The change of shape occurs at points a and b. The position of a and b on the FE (and then across to the EE) is found by projecting down to the FE via the end of the hexagonal prism (follow the arrows).

The intersection on the FE can then be completed. A square prism meeting a square pyramid at right angles ( Fig. 12.6 ). The EE shows where corners 1 and 3 meet the pyramid. These are projected across to the FE. Corners 2 and 4 are not quite so obvious. The pictorial view shows how these corners meet the pyramid. If the pyramid was cut across X – X, the section of the pyramid resulting would be square, and points 2 and 4 would lie on this square.

It is not necessary to make a complete, shaded section on your drawing but it is necessary to draw the square on the plan. Since points 2 and 4 lie on this square it is simple to find their exact position. Project corners 2 and 4 from the EE onto the plan. The points where these projectors meet the square are the exact positions of the intersections of corners 2 and 4 with the pyramid.

Third angle projection 2 3 4 1 2, 4 4 2 1 3 X X 3 1 Pictorial view with part above X–X removed 2 4 Figure 12.6 A square pyramid and a hexagonal prism meeting at an angle ( Fig. 12.7 ). The FE shows where corners 1 and 4 meet the pyramid. Corners2 and 6 lie on the same plane X – X. If this plane is marked on the plan view of the pyramid (follow the arrows) it results in the line X – X – X. Corners 2 and 6 lie on this plane; their exact positions are as shown. www.engbookspdf.com Intersection of Regular Solids 169 First angle projection 6 1 1 2 X X Y Y 6 3 5 2 3 X Y 4 6 5 1 4 2 3 5 4 Y X X Y Figure 12.7 Corners3 and 5 lie on the same plane Y – Y. On the plan view this plane is seen as the line Y – Y – Y (follow the arrows). Corners 3 and 5 lie on this plane; their exact positions are as shown.

Two dissimilar cylinders meeting at right angles ( Fig. 12.8 ). The smaller cylinder is divided into 12 equal sectors on the FE and on the plan (the EE shows how these are arranged round the cylinder). Theplan shows where these sectors meet the larger cylinder and these intersections are projected down to the FE to meet their corresponding sector at 1  , 2  , 3 , etc.